I Fought Galois and Galois Won

Good Morning!

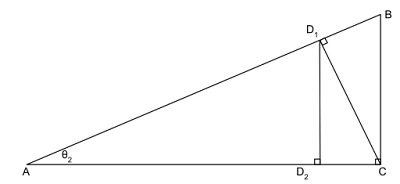
My sophomore year in high school (1991-1992), while I was learning about right triangles, geometric means, and similar triangles, I asked myself what I thought was a fairly simple and obvious question; if I continue to draw the altitudes for the new triangles formed by the original altitude, will I ever get triangles that are congruent in addition to being similar? For those who are not math-savvy, congruence is a stronger form of similarity. The following images illustrate the idea.

The first altitude.

The second altitude.

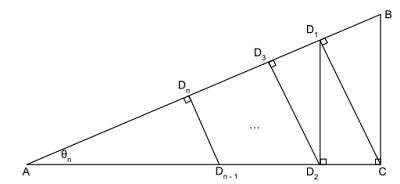The nth altitude.

My question is about when triangle CBD₁ is congruent to triangle AD_n-1D_n.

Using some basics of trigonometry, over the years I was able to write a polynomial equation that I could use to answer my question. In fact, I was able to determine that there was a specific right triangle which produced congruent triangles with the first altitude. Then, using the quadratic formula, I was able to determine a specific triangle which produced congruent triangles with the second altitude. Using formulas for solving cubic and quartic equations, I was able to find the triangles for the third and fourth altitudes as well. The solutions are not pretty, but they exist. For reference, the equations that produce the solutions are of the form xⁿ + x - 1 = 0.

About 20 years ago I posted in an online forum about the case for the fifth altitude, which could be solved if I could find a solution for the corresponding 5^th degree polynomial equation. The response I got made no sense to me; "the Galois group for the polynomial suggests it isn't solvable." I would later find out that my specific polynomial was solvable. The issue with Galois theory is that, in general, 5^th degree (and higher) polynomials are not solvable in the same way that quadratics and cubics and quartics are solvable. That is, there generally won't be a formula using the basic operations of mathematics for solving polynomial equations of degree greater than 4. I found the solution for the case n = 5, but this is likely where Galois theory wins the battle. It is unlikely that formulaic solutions (similar to the quadratic formula) can be found for n > 5.

In my last class for my Master's Degree, Survey of Algebra, I had the opportunity to turn my work on this problem into my final project for the course since Galois Theory was one of the topics covered in the course. One of the things I was able to accomplish with this project was to show that for any natural number n, there exists a right triangle such that the triangles produced by the n^th altitudes are congruent. This is what is known as an existence theorem. It demonstrates that under these circumstances a solution does exist, but makes no claims as to how one might go about finding it.

For a detailed look at the problem and the corresponding proof, I point you to this document which allows better math notation that Blogger does.

In any event, 

THEOREM: For any natural number n, there exists a right triangle such that the n^th altitude created in the manner shown above gives triangle CBD₁ congruent to triangle AD_n-1D_n.